岁末年初的财报季或是“年终奖季”，很多新闻往往会写着“某上市公司人均收入如何如何”、“某城市年人均工资如何如何”的标题，其实这里面可能存在着误读。

　　好，让我们来一步步分析。

　　烧脑的平均工资

　　平均数引发的“被平均”讨论或是“标题党”，早已屡见不鲜。如某互联网大咖企业2019年Q1财报显示，员工人数5.46万，薪酬支出为116亿元，由此一些媒体计算并制造出“某公司员工平均月薪7万元”的轰动新闻，不仅读者沸腾，很多该公司员工也直呼自己“被平均了”。

　　同样，NBA联赛的球员工资也是如此。以2018-19赛季为例，NBA球员平均工资是617万美元，总计有588名球员纳入工资统计(包括双向合同、十天断约和延期支付等)。

　　看起来是绝对不可思议的高薪，但其中有402人的薪资未到平均水准，占总数的68%。321人连薪资平均值的一半都没到，而工资榜前100名的球员，占全体球员工资总额比重达到57%，即接近60%的工资集中在不到20%的球员手中。

　　是否发现，平均值往往看起来很不错，那么原因究竟是什么呢？

　　三个重要概念

　　我们先来区分一下三个重要的统计概念，分别是平均数、中位数和众数。

　　(1)平均数

　　平均数在本文中特指算术平均数，即一组数据用总和除以总数据个数，得出的数就是这组数据的算术平均数。平均数的大小与一组数据里的每个数据都有关系，任何一个数据的变动都会引起平均数的变动，即平均数易受较大数和较小数的影响。

　　(2)中位数

　　中位数是将一组数据按大小依次排列，选择最中间位置的一个数(或最中间位置的两个数的平均数)。中位数的大小仅与数据的排列位置有关。因此中位数不受偏大和偏小数的影响，当一组数据中的个别数据变动较大时，可以描述这组数据的集中趋势。

　　(3)众数

　　众数是在一组数据中出现次数最多的数据。求一组数据的众数既不需要计算，也不需要排序，只需寻找出现次数较多的数据。

　　众数与概率有密切的关系。众数的大小仅与一组数据中的部分数据有关。当一组数据中有不少数据多次重复出现时，众数往往就是一种集中的趋势。

　　让我们通过一个案例来方便理解。

　　假设一个团队，有9个人，我们用A-I的字母来代表每个人，收入如下表：

　　通过简单的计算和分析，我们得出三个统计量，如下所述：

　　平均数：9000(所有人收入相加然后除以人数，可以得出平均数9000)

　　中位数：7000(排序，居中者为7000)

　　众数：5000(出现最多的数，有3人的收入为5000)

　　正态和偏态

　　正态分布，大家可能不会陌生，但是否想过或是从之前的例子中已经看出一些端倪，即现实生活中的很多分布，并不完全是正态分布的，即平均数、中位数、众数之间存在差值，整体分布的高峰位于一侧，尾部向另一侧延伸，这就是与“正态分布”相对的“偏态分布”。

　　偏态分布是分布曲线左右不对称的数据分布，分为正偏态和负偏态。

　　先不必头晕，其实我们很容易记住和辨别。

　　(1)正偏态分布

　　平均数大于中位数，中位数又大于众数的数据分布。特征是曲线的最高点偏向X轴的左边，位于左半部分的曲线比正态分布的曲线更陡，而右半部分的曲线比较平缓，并且其尾线比起左半部分的曲线更长，无限延伸直到接近X轴

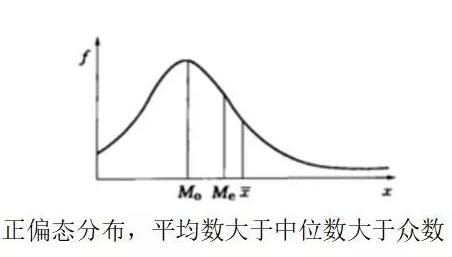
　　从之前的例子可以发现，工资这类的分布往往就是正偏态分布。

　　(2)负偏态分布

平均数小于中位数，中位数又小于众数的数据分布。特征是曲线的最高点偏向X轴的右边，位于右半部分的曲线比正态分布的曲线更陡，而左半部分的曲线比较平缓，并且其尾线比起右半部分的曲线更长，无限延伸直到接近X轴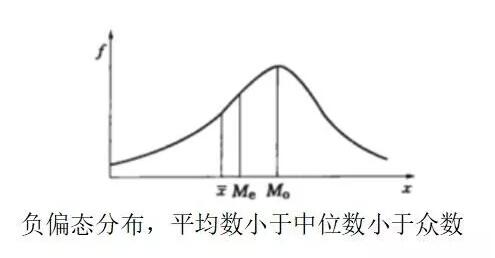

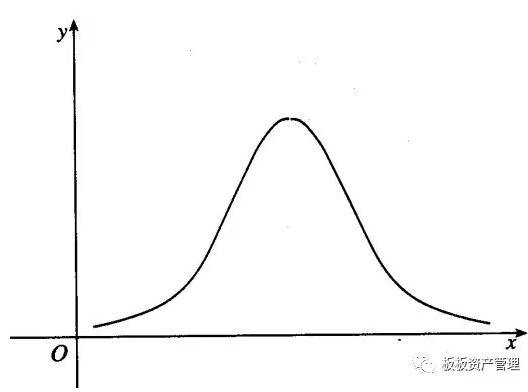
　　(3)正态分布

　　最后，我们再来看看正态分布，此时的平均数、中位数和众数都位于对称中心，三者相等。正态分布其实可以看作是偏态分布的一个特例。

　　其实只需记住一个工资案例，就可以理解这些烧脑概念。

　　在各类不存在负数的样本中，往往是一头(比如最低工资)是有底部的，而另一头往往非常大(比如收入高的可能高到超过最低者很多数量级)。

　　以工资为例，正常职员是不会存在负数工资情况的，即每个月正常工作不仅没有收入还要倒贴钱，但市场化的工资上限往往可以非常高。因此，少数极其高的工资自然就拉高了平均工资，也使得平均工资往往超过了大部分人的实际工资。因此现实生活其实就是这样，每次媒体公布平均工资，自然会有很多人在评论区大呼“我拖后腿了，我被平均了!”

　　反之，如果很多人都觉得自己的工资比平均工资高，那么必须存在一些极其低的工资去拉低平均数，但由于工资不可能存在负数甚至不可能存在极其低的工资(因为无人会去应聘)，因此通常不会出现此类情况。

　　实战应用心法

　　(1)判别可能对应的分布

　　通过逆向思维，我们在面对一个数据分布时，可以先计算平均数、中位数和众数，判断属于哪种分布，然后即可应用不同的心法。

　　现实生活中遇到的很多事物，往往偏态分布多于正态分布。那么当平均数、中位数、众数不同时，如何使用这三个统计量呢？我们得根据研究对象的具体情况，看哪个统计量最能反映这组数据的一般水平。

　　平均数非常明显的优点是能够用到所有数据的特征，而且容易计算。但平均数有不足之处，即用到了所有数据的信息，易受极端数据的影响。

　　中位数和众数这两个统计量的特点都能够避免极端数据，但缺点是没有完全利用数据所反映出的信息。

　　(2)考虑忽略最低和最高

　　我们常见的很多比赛评分，往往会去除一个最高分和一个最低分，那么这是为什么呢？

　　当我们用平均数来表示一个数据的“集中趋势”时，如果数据中出现一两个极端数据，那么平均数对于这组数据所起的代表作用就会削弱，为了消除这种现象，可去除少数极端数据，只计算余下数据的平均数，把所得的结果作为全部数据的平均数。

　　因此，大量的文艺与体育比赛的打分成绩计算时，常常采用在评分数据中分别去除一个(或两个)最高分和一个(或两个)最低分，再计算其中平均分的办法，以避免极端数据造成的不良影响。

　　我们继续用逆向思维，即多关注中位数和众数，在很多情况下，中位数和众数可能更能体现实际的分布，比如之前收入例子中的“H”，此人的收入(28000)遥遥领先，拉高了平均数(9000)，但中位数(7000)和众数(5000)可能更符合这群人的实际收入分布。

　　(3)尽量投资和跟随平均数

　　平均数只是描述一个总体的一个指标，当总体分布相对均匀时，平均数是有意义的，而当其分布不均匀时，用平均数试图描述个体就不太适合了。

　　但，逆向思维给我们的灵感是如果现实生活中很多事物都是正偏态分布，尤其在投资领域，那么我们为何不直接投资和跟随平均数呢?

　　比如投资收益率就是明显的正偏态分布，即平均数(指数收益率)大于中位数，中位数又大于众数(大部分投资者收益率)。

　　可延伸阅读之前这篇《烧脑|为什么绝大多数投资者会被指数暴击？》。

　　同样，大多数人的收入在平均水平之下也完全符合数学，根本原因就是收入特别高的人对平均数的贡献往往实在太大。因此，如果允许全部就业者选择领取平均工资(之前例子中的平均数9000，战胜了9人中的7人，还战平了第2名的收入，仅败给了第1名H的收入28000)，我想不少人会非常愉快和欣然地接受。

　　最后，用一句调侃的话来帮助我们记住平均数可能带来的思考错误吧。

　　“嗯，巴菲特的确有钱，查理·芒格和我加起来还没有他老人家多。”

　　延伸思考

　　期望值在投资领域真的很有用吗？

　　这个问题会在以后的分享中进行推导，谢谢您的鼓励的支持！

　　同时，您还想一起思考哪些现象背后的算法？欢迎您畅所欲言，一起好好聊聊。